Definisi Parabola Beserta Bagian-Bagiannya
Parabola adalah tempat kedudukan
titik-titik yang jaraknya ke satu titik tertentu sama dengan jaraknya ke sebuah
garis tertentu (direktriks).
Dalam bidang
Matematika, sebuah parabola adalah bagian kerucut yang merupakan irisan antara
permukaan suatu kerucut melingkar dengan suatu bidang datar. Parabola ini dapat
dinyatakan dalam sebuah persamaan.
Atau secara
umum, sebuah parabola adalah kurva yang mempunyai persamaan.
sehingga,
Perhatikan gambar berikut :
Berikut
bagian-bagian dari Parabola :
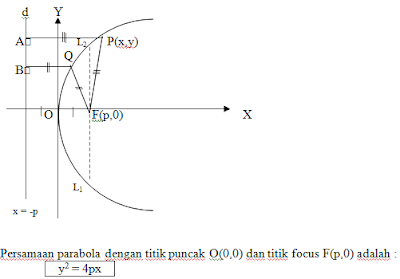
1. Persamaan Parabola dengan Puncak O(0,0)
Keterangan:
– Titik O(0,0) adalah titik puncak parabola
– Titik F(p,0) adalah titik fokus parabola
– Garis x = -p adalah garis direktriks
– Sumbu X adalah sumbu simetri
– L1L2 adalah lactus rectum = 4p
Parabola terbuka ke kanan
2. Persamaan Parabola dengan Puncak P(a,b)
Perhatikan gambar berikut ini !
Keterangan :
- titik puncak
P(a,b)
- titik fokus
F(a + p, b)
- persamaan
direktriks : x = a – p
- persamaan
sumbu simetri : y = b
Parabola terbuka ke kanan.
Langkah-Langkah
Membuat Grafik Parabola Beserta Contoh Soal
1. Langkah-langkah Membuat Grafik
Parabola
Parabola
adalah kurva simetris dua dimensi yang berbentuk seperti irisan kerucut. Semua
titik dalam parabola berjarak sama dari titik fokus dan garis directrix.
Untuk membuat grafik parabola, Anda harus menemukan titik puncak juga beberapa
koordinat x dan y di kedua sisi titik puncak parabola untuk menandai jalur yang
dilewatinya.
Pahami bagian grafik parabola. Anda mungkin diberikan beberapa
informasi sebelum menggambar grafik parabola, dan mengetahui istilahnya akan
membantu Anda menghindari langkah yang tidak diperlukan. Berikut ini adalah
bagian-bagian grafik parabola yang perlu Anda ketahui:
- Titik
fokus. Titik
tetap di bagian dalam parabola yang digunakan untuk mendefinisikan kurva.
- Titik
directrix. Garis
lurus tetap. Parabola adalah himpunan titik-titik yang berjarak sama dari
titik fokus dan titik directrix.
- Sumbu
simetri. Sumbu
simetri adalah garis vertikal yang berpotongan dengan titik balik
parabola. Setiap sisi sumbu simetri adalah bayangan cermin.
- Titik puncak parabola. Titik perpotongan antara sumbu simetri dengan parabola. Jika parabola membuka ke atas, titik ini disebut sebagai titik minimal, sedangkan jika terbuka ke atas, titik ini disebut sebagai titik maksimal.
Pahami persamaan perabola. Persamaan parabola adalah y = ax2+
bx + c. Persamaan ini juga dapat dituliskan y = a(x – h)2 + k.
Namun, kita akan menggunakan persamaan yang pertama dalam contoh di sini.
- Jika
variabel a dalam persamaan bernilai positif, parabola akan membuka
ke atas, seperti huruf "U", dan mempunyai nilai minimal. Jika a
bernilai negatif, parabola akan membuka ke bawah dan mempunyai nilai
maksimal. Untuk membantu mengingatnya, bayangkan bentuk parabola seperti
senyuman jika a bernilai positif, dan bentuk parabola seperti
cemberut jika a bernilai negatif.
- Sebagai
contoh pada persamaan: y = 2x2 -1. Parabola ini akan
berbentuk seperti huruf "U" karena variabel a bernilai
positif, yaitu 2.
- Jika
ada variabel y kuadrat dan bukan x kuadrat dalam persamaan Anda, parabola
akan membuka ke samping, ke kanan atau ke kiri, mirip seperti huruf
"C" atau "C" terbalik. Misalnya, parabola x2
= y + 3 membuka ke kanan, seperti huruf "C".
Cari sumbu simetri parabola. Ingatlah bahwa sumbu simetri ini
adalah garis vertikal yang berpotongan dengan titik balik parabola. Koordinat x
titik ini sama dengan titik puncak, yang merupakan perpotongan antara sumbu
simetri dengan parabola. Untuk mencari sumbu simetri parabola, gunakan
persamaan: x = -b/2a
- Dari
persamaan contoh, diketahui a = 2, b = 0, dan c = 1.
Sekarang, Anda bisa menghitung sumbu simetri dengan memasukkan nilai di
atas ke dalam persamaan: x = -0/(2 x 2) = 0.
- Sumbu simetri parabola adalah x = 0.
Cari titik puncak parabola. Setelah mendapatkan sumbu simetri
parabola, Anda bisa memasukkan nilai yang diperoleh dalam persamaan di atas
untuk mendapatkan nilai y pasangannya. Titik koordinat yang dihasilkan adalah
titik puncak parabola. Dalam contoh di sini, Anda harus memasukkan nilai 0 ke
dalam persamaan 2x2 -1 untuk mendapatkan nilai y, y = 2 x 02
-1 = 0 -1 = -1. Jadi, titik puncak parabola Anda adalah (0,-1), yang merupakan
titik perpotongan parabola dengan sumbu y.
- Koordinat
titik puncak juga disebut sebagai (h, k). Nilai h adalah 0 dan k
adalah -1. Jika persamaan parabola ini dituliskan dalam bentuk y = a(x
– h)2 + k, titik puncak parabola adalah (h, k), dan Anda tidak harus
menghitungnya terlebih dahulu, asalkan dapat memahami grafik dengan benar.
Buat tabel berisi nilai x. Dalam langkah ini, Anda harus
membuat tabel dan memasukkan nilai x di kolom yang pertama. Tabel ini akan
memberikan koordinat yang diperlukan untuk menggambar grafik parabola.
- Titik
tengah x adalah sumbu simetri parabola.
- Agar
simetri, Anda sebaiknya menyertakan 2 nilai di atas dan di bawah nilai
tengah x ke dalam tabel.
- Sesuai
contoh, masukkan nilai sumbu simetri x = 0, ke tengah tabel.
Hitung nilai koordinat y. Masukkan setiap nilai x ke dalam
persamaan parabola dan hitung nilai y pasangannya. Masukkan nilai y yang
diperoleh ke dalam tabel. Sesuai contoh, persamaan parabola dihitung sebagai
berikut:
- Untuk x
= -2, y dihitung sebagai berikut: y = 2 x (-2)2 - 1 = 8
- 1 = 7
- Untuk x
= -1, y dihitung sebagai berikut: y = 2 x (-1)2 - 1 = 2
- 1 = 1
- Untuk x
= 0, y dihitung sebagai berikut: y = 2 x (0)2 - 1 = 0 -
1 = -1
- Untuk x
= 1, y dihitung sebagai berikut: y = 2 x (1)2 - 1 = 2 -
1 = 1
- Untuk x
= 2, y dihitung sebagai berikut: y = 2 x (2)2 - 1 = 8 -
1 = 7
Masukkan hasil
perhitungan nilai y ke dalam tabel. Setelah mendapatkan paling tidak 5
titik koordinat parabola, Anda nyaris siap menggambarnya. Sesuai hasil
perhitungan, Anda sekarang mempunyai 5 titik: (-2, 7), (-1, 1), (0, -1), (1,
1), (2, 7). Sekarang, ingat kembali bahwa parabola adalah bayangan cermin di
sumbu simetrinya. Berarti, koordinat titik y dari koordinat titik x yang saling
berseberangan pada sumbu simetri bernilai sama. Koordinat y dari koordinat x -2
dan 2 adalah 7, dan seterusnya.
Gambarkan titik yang tercantum dalam
tabel ke dalam bidang koordinat. Setiap baris tabel membentuk titik koordinat (x, y)
di bidang koordinat. Jadi, gambarlah semua titik koordinat yang tercantum dalam
tabel ke bidang koordinat.
- Sumbu x
merupakan sumbu horizontal, sedangkan sumbu y merupakan sumbu vertikal.
- Nilai y
positif terletak di atas titik (0, 0) dan nilai y negatif terletak di
bawah titik (0, 0).
- Nilai x
positif terletak di sisi kanan titik (0, 0) dan nilai x negatif terletak
di sisi kiri titik (0, 0).
Hubungkan titik
di bidang koordinat.
Untuk membuat grafik parabola, hubungkan titik-titik yang diperoleh dalam
langkah sebelumnya. Grafik dari persamaan contoh akan berbentuk seperti huruf
U. Pastikan untuk menghubungkan titik-titik dengan garis lengkung, bukan garis
lurus. Dengan begitu, akan diperoleh grafik parabola yang akurat. Anda juga
bisa menggambar anak panah ke atas atau ke bawah di kedua ujung parabola,
sesuai bentuk grafik. Hal ini menandakan grafik parabola akan terus membesar
hingga keluar bidang koordinat.
Contoh Soal Dan Pembahasan Parabola
1. Tentukan persamaan parabola jika titik puncaknya (2, 3) dan titik fokusnya (6, 3) !
Jawab:
Puncak (2, 3) dan focus (6, 3), maka : p = 6 – 2 = 4
Persamaan parabolanya :
(y – b)2 = 4p(x – a)
(y – 3)2 = 4.4(x – 2)
y2 – 6y + 9 = 16(x – 2)
y2 – 6y + 9 = 16x – 32
y2 – 6y – 16x + 41 = 0
2. Diketahui persamaan parabola sebagai berikut : y2 + 4y – 4x + 8 = 0.
Tentukan koordinat puncak , koordinat focus, persamaan sumbu simetri, persamaan direktriks, dan sketsa gambarnya !
Jawab:
y2 + 4y – 4x + 8 = 0
y2 + 4y = 4x – 8
(y + 2)2 – 4 = 4x – 8
(y + 2)2 = 4x – 4
(y + 2)2 = 4(x – 1) = (y – b)2 = 4p(x – a)
Berarti : b= -2; a= 1; p = 1
Jadi, koordinat puncaknya (1, -2), koordinat fokusnya (a + p,b) = (2, -2), persamaan sumbu simetrinya y = -2, dan persamaan garis direktriksnya : x = a – p.
x = 1 – 1 = 0
Grafiknya :
Demikian penjelasan tentang definisi parabola beserta langkah-langkahnya. Semoga bermanfaat :)